Porotaxis: Cell Migration in Disordered Media

L. Würthner (Contributor)

Persistent Identifier

Use this permanent link to cite or share this Morpheus model:

Cell migration in disordered fibrous porous media

Introduction

We present a Morpheus model for amoeboid cell migration in disordered porous environments. The simulation domain consists of fibrous porous media, which resemble the natural environment of many cell types. The model allows to investigate how spatial confinement and disorder influences the mode of cell motility.

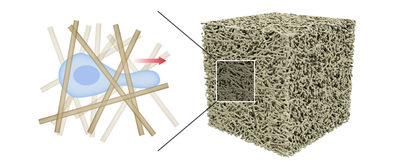
**Figure 1.** Active Brownian motion (ABM) in disordered environments.

Description

In the following, we outline the basic components of the model.

Active Brownian motion

Cell motility is described via Active Brownian motion (ABM) – a well known model that characterizes the self-propulsion of active (energy consuming) systems.

Each cell is assigned a polarity vector $\mathbf{\hat{p}}(t)$ of unit length which dictates the run direction at time $t$. The temporal evolution of the components of the polarity vector are governed by stochastic differential equations (SDEs)

$$\frac{d}{dt} \hat{\mathbf{p}} = \sqrt{2D_r} \ \hat{\mathbf{p}} \times \boldsymbol{\xi}(t)$$

where $\boldsymbol{\xi(t)}$ describes uncorrelated Gaussian white noise. Since we require the polarity vector to be of unit length, the noise is interpreted in the Stratonovich sense, and the cross product $\times$ is thus to be interpreted as a Stratonovich product. The polarity vector evolves via rotational diffusion on the unit sphere with a rate given by the rotational diffusion coefficient $D_r$. Since Morpheus requires the SDEs in Itô form, we use spherical coordinates and reduce the dynamics of the polarity vector to equivalent Itô SDEs for the azimuthal and polar angles $\varphi(t)$ and $\theta(t)$ (details presented in the paper).

Coupling to CPM

The dynamics of the polarity vector must be coupled to CPM dynamics. This is achieved through the convenient built-in plugin DirectedMotion in Morpheus. This plugin introduces an additional term in the Hamiltonian

$$\mathcal{H}_p = -\mu \sum_\sigma \hat{\mathbf{p}}_\sigma \ \mathbf{x}_\sigma$$

which leads to a bias of CPM lattice updates $\mathbf{x}_\sigma$ in direction of the polarity vector and thus active cell motility.

Fibrous porous media (TIFF images)

The simulation geometries consist of randomly oriented cylindrical fibers with fixed radius and length. We created these geometries using PoreSpy, a freely available open source Python package for generation and analysis of porous materials. PoreSpy provides the generated porous geomeries as voxel images in TIFF format, which can be readily imported as simulation domain in the Morpheus model.

The model treats the cylindrical fibers as rigid obstacles by employing no-flux boundary conditions at fiber surfaces.

We provide two examples of geometries:

disordered-fibrous-media-porosity-065.tiff

Fibrous porous geometry with porosity $\phi = 0.65$ and dimensions $L_x=L_y=L_z=400$. Here, the domain boundary conditions have been set to periodic in x, y, and z to mimic an infinitely large system.
disordered-fibrous-step-gradient.tiff

Heterogeneous fibrous porous media with dimensions $L_x=L_y=100$ and $L_z=300$. The porosity is spatially varying and exhibits a step-like profile where $\phi=0.7$ for $z < 100$ and $z > 200$, while $\phi=0.62$ for $100<z<200$. The domain is periodic along x and y, but closed (no-flux) in z, such that the dynamics can reach a steady state probability distribution of cell positions (porotaxis).

Visualization in ParaView

To generate simulation movies, we export the Morpheus simulations in the VTK file format. These files can be imported and visualized in the freely available software ParaView.

Video 1. Cellular hopping and trapping in disordered media. Cell migration is not persistent due to confinement. Instead, cells must migrate through the geometry by hopping from one pore to another. The time they spent in a pore (trapping time) and the distance traveled during hops (hop length) are fingerprints that reveal the mode of cell motility.

Video 2. Porotaxis in heterogeneous porous media. Spatial gradients result in spatial variations of the mean trapping time, effectively resulting in directed cell motion towards low porosity regions (stronger confinement).

Reference

This model is the original used in the publication, up to technical updates:

L. Würthner, F. Graw: Geometry of disordered porous environments regulates cell migration. Phys. Rev. E, 2026.

Model

Get this model via:

Morpheus-Link or

Download: cell-migration-fibrous-media_main.xml

XML Preview

<?xml version='1.0' encoding='UTF-8'?>
<MorpheusModel version="4">
    <Description>
        <Title>Cell migration in disordered fibrous porous media</Title>
        <Details>Model ID:	https://identifiers.org/morpheus/M9342
  File type:	Main model
  Software:	Morpheus (open source). Download from: https://morpheus.gitlab.io
Full title:	Porotaxis: Cell Migration in Disordered Media 
Authors:	L. Würthner, F. Graw
Submitter:	L. Würthner
Curator:	D. Jahn
Date:	03.11.2025
Reference:	This model is the original used in the publication, up to technical updates:
	L. Würthner, F. Graw: Geometry of disordered porous environments regulates cell migration. Phys. Rev. E, 2026.
	https://doi.org/10.1103/hvtd-qwp1
Comment:	Cell migration in disordered media with fixed material porosity and periodic boundary conditions.</Details>
    </Description>
    <Global>
        <Constant symbol="cell_vol" name="cell volume" value="2500"/>
        <Constant symbol="cell_surf" name="cell surface (aspherity)" value="1.1"/>
        <Constant symbol="motion_str" name="ABM bias strength" value="3"/>
        <Constant symbol="Dr" name="ABM rotational diffusion coefficient (in 3D Dr=1/(2*persistence_time))" value="1/600"/>
        <Constant symbol="dt" name="integration step size for SDEs" value="0.1"/>
        <Constant symbol="mcs" name="Monte Carlo time scale" value="1"/>
        <Constant symbol="Ncells" name="Total number of simulated cells" value="50"/>
    </Global>
    <Space>
        <Lattice class="cubic">
            <Size symbol="size" value="400,400, 400"/>
            <Neighborhood>
                <Order>optimal</Order>
            </Neighborhood>
            <BoundaryConditions>
                <Condition type="periodic" boundary="x"/>
                <Condition type="periodic" boundary="y"/>
                <Condition type="periodic" boundary="z"/>
            </BoundaryConditions>
            <Domain boundary-type="noflux">
                <Image path="disordered-fibrous-media-porosity-065.tiff"/>
            </Domain>
        </Lattice>
        <SpaceSymbol symbol="space"/>
    </Space>
    <Time>
        <StartTime value="0"/>
        <StopTime value="1e6"/>
        <TimeSymbol symbol="time"/>
    </Time>
    <CellTypes>
        <CellType class="medium" name="medium"/>
        <CellType class="medium" name="ecm"/>
        <CellType class="biological" name="cell">
            <VolumeConstraint strength="1" target="cell_vol"/>
            <PropertyVector notation="x,y,z" symbol="move_dir" value="sin(theta)*cos(phi),sin(theta)*sin(phi),cos(theta)"/>
            <DirectedMotion retraction="false" strength="motion_str" protrusion="true" direction="move_dir"/>
            <SurfaceConstraint strength="1.5" target="cell_surf" mode="aspherity"/>
            <System time-step="dt" solver="Euler-Maruyama [stochastic, O(1)]">
                <DiffEqn symbol-ref="phi">
                    <Expression>sqrt(2*Dr/dt)/sin(theta)*rand_norm(0,1)</Expression>
                </DiffEqn>
                <DiffEqn symbol-ref="theta">
                    <Expression>Dr/tan(theta)+sqrt(2*Dr/dt)*rand_norm(0,1)</Expression>
                </DiffEqn>
                <VectorRule symbol-ref="move_dir" notation="x,y,z">
                    <Expression>sin(theta)*cos(phi),sin(theta)*sin(phi),cos(theta)</Expression>
                </VectorRule>
            </System>
            <Property symbol="phi" value="rand_uni(0,2*pi)"/>
            <Property symbol="theta" value="rand_uni(0.1,pi)"/>
        </CellType>
    </CellTypes>
    <CPM>
        <Interaction default="0">
            <Contact value="0" type1="cell" type2="medium"/>
            <Contact value="10" type1="cell" type2="cell"/>
            <Contact value="0" type1="cell" type2="ecm"/>
        </Interaction>
        <MonteCarloSampler stepper="edgelist">
            <MCSDuration value="mcs"/>
            <Neighborhood>
                <Order>1</Order>
            </Neighborhood>
            <MetropolisKinetics temperature="2"/>
        </MonteCarloSampler>
        <ShapeSurface scaling="norm">
            <Neighborhood>
                <Order>optimal</Order>
            </Neighborhood>
        </ShapeSurface>
    </CPM>
    <CellPopulations>
        <BoundaryValue type="value" boundary="domain" value="ecm"/>
        <Population type="cell" size="1">
            <InitRectangle number-of-cells="Ncells" mode="random">
                <Dimensions origin="0, 0, 0" size="size.x, size.y, size.z"/>
            </InitRectangle>
        </Population>
    </CellPopulations>
    <Analysis>
        <Logger time-step="50">
            <Input>
                <Symbol symbol-ref="cell.center.x"/>
                <Symbol symbol-ref="cell.center.y"/>
                <Symbol symbol-ref="cell.center.z"/>
            </Input>
            <Output>
                <TextOutput file-separation="cell"/>
            </Output>
            <Restriction>
                <Celltype celltype="cell"/>
            </Restriction>
        </Logger>
        <ModelGraph format="svg" reduced="false" include-tags="#untagged"/>
        <VtkPlotter time-step="100" mode="binary">
            <Channel symbol-ref="cell.type" exclude-medium="true"/>
        </VtkPlotter>
    </Analysis>
</MorpheusModel>

This model requires two external files:

disordered-fibrous-media-porosity-065.tiff, which must be in the same directory as cell-migration-fibrous-media_main.xml, and
disordered-fibrous-step-gradient.tiff, which must be in the same directory as cell-migration-fibrous-media-porotaxis.xml.

Downloads

Files associated with this model:

Last updated on Fri, 23 Jan 2026