Logistic Proliferation
Persistent Identifier
Use this permanent link to cite or share this Morpheus model:
How to dynamically regulate individual cell proliferation?
Introduction
Proliferation of individual cells may be coupled through the dependence on common resources. This turns the otherwise exponential growth of the population size into, for example, logistic growth. Stem cell populations in their niche may be modeled this way such that a bounded population size of stem cells results and generates a constant flux of differentiated cells. The latter scenario was motivated by Mavis in the User Forum and is picked up in this model.
Description
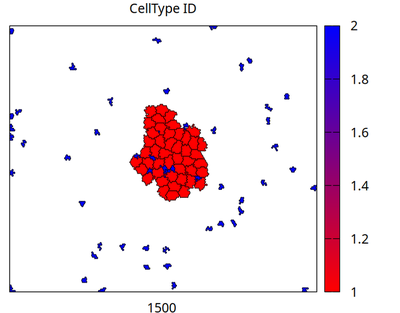
The model considers two cell types, stem cells (red) and differentiated cells (blue). Stem cells proliferate with a rate ‘r*(1-N_SC/K)’ where ‘r’ is the maximum division rate of an isolated cell, ‘N_SC’ is the number of coupled stem cells (provided by Morpheus through the Symbol ‘celltype.stem_cell.size’) and ‘K’ is the carrying capacity of the niche. Differentiated cells, just for illustration, shrink their volume and migrate outward. Differentiation occurs with rate ’d'. The parameters ‘r’, ‘K’ and ’d' can be set in the ‘Global’ section of the model. The simulation is initialized with a single stem cell in the center.
Results
Movie: Simulation of the logistic proliferation of individual cells (red) and differentiation into migrating cells (blue).
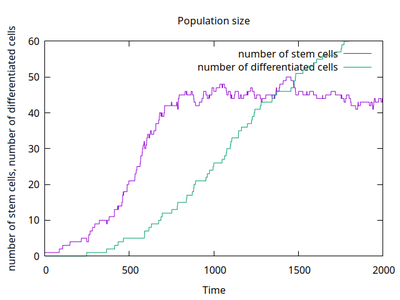
The number of simulated stem cells can be counted (purple in the time course plot) and shows the emergent balance of proliferation (coupled through a common carrying capacity) and differentiation. Also the number of differentiated cells is counted (green curve) and shows a linear increase after the stem cell population has reached its balance.
Model
Logistic_Proliferation.xml
XML Preview
<?xml version='1.0' encoding='UTF-8'?>
<MorpheusModel version="4">
<Description>
<Details></Details>
<Title>Logistic_Proliferation</Title>
</Description>
<Space>
<Lattice class="hexagonal">
<Neighborhood>
<Order>optimal</Order>
</Neighborhood>
<Size symbol="size" value="200, 200, 0"/>
<BoundaryConditions>
<Condition type="noflux" boundary="x"/>
<Condition type="noflux" boundary="y"/>
</BoundaryConditions>
</Lattice>
<SpaceSymbol symbol="space"/>
</Space>
<Time>
<StartTime value="0"/>
<StopTime value="2000"/>
<TimeSymbol symbol="time"/>
</Time>
<Analysis>
<ModelGraph include-tags="#untagged" format="dot" reduced="true"/>
<Gnuplotter time-step="100">
<Plot>
<Cells max="2" min="1" value="cell.type">
<ColorMap adaptive-range="false">
<Color color="red" value="1"/>
<Color color="blue" value="2"/>
</ColorMap>
</Cells>
</Plot>
<Terminal name="png"/>
</Gnuplotter>
<Logger time-step="1.0">
<Input/>
<Output>
<TextOutput/>
</Output>
<Plots>
<Plot title="Population size" time-step="-1">
<Style style="lines"/>
<Terminal terminal="png"/>
<X-axis>
<Symbol symbol-ref="time"/>
</X-axis>
<Y-axis minimum="0" maximum="60">
<Symbol symbol-ref="N_stem_cell"/>
<Symbol symbol-ref="N_differentiated_cell"/>
</Y-axis>
</Plot>
</Plots>
</Logger>
<Function symbol="N_stem_cell" name="number of stem cells">
<Expression>celltype.stem_cell.size</Expression>
</Function>
<Function symbol="N_differentiated_cell" name="number of differentiated cells">
<Expression>celltype.differentiated_cell.size</Expression>
</Function>
</Analysis>
<Global>
<Constant symbol="r" name="proliferation rate" value="0.01"/>
<Constant symbol="K" name="carrying capacity" value="50"/>
<Constant symbol="d" name="differentiation rate" value="0.001"/>
</Global>
<CellTypes>
<CellType name="medium" class="medium"/>
<CellType name="stem_cell" class="biological">
<VolumeConstraint target="50" strength="1"/>
<SurfaceConstraint target="0.9" strength="1" mode="aspherity"/>
<ConnectivityConstraint/>
<CellDivision name="logistic proliferation" division-plane="major">
<Condition>rand_uni(0,1) < r*(1-celltype.stem_cell.size/K)*mcs_duration</Condition>
</CellDivision>
<ChangeCellType time-step="mcs_duration" newCellType="differentiated_cell" name="differentiation">
<Condition>rand_uni(0,1) < d*mcs_duration</Condition>
</ChangeCellType>
</CellType>
<CellType name="differentiated_cell" class="biological">
<VolumeConstraint target="10" strength="1"/>
<SurfaceConstraint target="0.8" strength="2" mode="aspherity"/>
<ConnectivityConstraint/>
<DirectedMotion strength="0.5" name="motility" direction="cell.center.x-size.x/2, cell.center.y-size.y/2, 0"/>
</CellType>
</CellTypes>
<CellPopulations>
<Population type="stem_cell" size="1">
<InitCellObjects mode="distance">
<Arrangement repetitions="1, 1, 1" displacements="1, 1, 1">
<Sphere center="size.x/2, size.y/2, 0" radius="4"/>
</Arrangement>
</InitCellObjects>
</Population>
</CellPopulations>
<CPM>
<Interaction>
<!-- <Disabled>
<Contact type2="medium" type1="stem_cell" value="5"/>
</Disabled>
-->
<!-- <Disabled>
<Contact type2="medium" type1="differentiated_cell" value="5"/>
</Disabled>
-->
<!-- <Disabled>
<Contact type2="differentiated_cell" type1="stem_cell" value="6"/>
</Disabled>
-->
<Contact type2="stem_cell" type1="stem_cell" value="-2"/>
<!-- <Disabled>
<Contact type2="differentiated_cell" type1="differentiated_cell" value="6"/>
</Disabled>
-->
</Interaction>
<ShapeSurface scaling="norm">
<Neighborhood>
<Order>optimal</Order>
</Neighborhood>
</ShapeSurface>
<MonteCarloSampler stepper="edgelist">
<MCSDuration symbol="mcs_duration" value="1"/>
<MetropolisKinetics temperature="1"/>
<Neighborhood>
<Order>optimal</Order>
</Neighborhood>
</MonteCarloSampler>
</CPM>
</MorpheusModel>

Downloads
Files associated with this model: