Caenorhabditis elegans L1 Aggregation
Persistent Identifier
Use this permanent link to cite or share this Morpheus model:
Introduction
Larvae of the nematode Caenorhabditis elegans aggregate into clusters of several hundred moving individuals when starved during their first larval stage (see video below). Avery et al. proposed that starved larvae produce and respond chemotactically to two diffusible chemical signals, a short-range attractant and a longer range repellent.
Video S1 as published in Avery et al., shows the aggregation dynamics of 500 000 starved C. elegans larvae over 12 hours (CC BY 4.0: Avery et al.).
Avery et al. have modelled worm motility and the proposed interaction in two different mathematical frameworks,
- continuous Keller-Segel-type partial differential equations (PDEs) of worm density with an additional repellent concentration field and
- a discrete individual-based Cellular Potts Model (CPM) in which each worm represents a stochastically and chemotactically moving
cellcoupled to PDEs for attractant and repellent.
Here, this hybrid CPM + PDE model for wild type worms is optimized for faster execution. This optimization and the parallel implementation of the CPM solver (from Morpheus version 2.3.0 onward) made it possible to simulate the full individual-based system of 72 000 interacting worms for the first time. Below, published results by Avery et al. are reproduced and new results for the full-scale system are presented.
Model Description
Avery et al. have shared their Cellular Potts Model of C. elegans L1 aggregation as Morpheus model file at GitHub. The authors' Morpheus model was inspired by a simpler Morpheus model of worm aggregation that Leah Edelstein-Keshet had developed, for details see second paragraph in the authors' README file. The published model was developed with Morpheus version 2.2.1 and the here provided and accelerated model was run in the newer Morpheus version 2.3.0 and is being tested with each latest version of Morpheus.
To accelerate model execution, the computation of observables that do not feed back on the system dynamics was separated from the frequent updates of the PDEs and moved to Analysis/Function where they get updated when needed for output. Also, CPM updates let the lattice configuration fluctuate from MCS to MCS and the source terms in the PDEs need not be updated with each fluctuation but could be kept constant over multiple MCS. Here, we’ve chosen to keep the source terms in the PDEs fixed for as many MCS as a worm occupies lattice nodes and chose the 4th order Runge-Kutta solver with a time-step of $1\ \mathrm{s}$. The CPM is updated in Monte Carlo steps of $0.15\ \mathrm{s}$. Worm target size is set to 5 lattice nodes as was calculated from the size of a real worm and the chosen lattice resolution with a node length of $0.0026\ \mathrm{cm}$ on a $2\ 304$ by $2\ 304$ square lattice. Altogether, the parallel implementation of the CPM solver (from Morpheus version 2.3.0 onward) and the above optimizations allowed to run the full-scale model within 2 days of runtime using 16 parallel threads and Linux OS. This works without interruption and does no longer require checkpointing and restarts, hence we have shifted the time interval from $1\ 500$ - $201\ 500$ back to $0$ - $200\ 000$. The time unit is second and the space unit is cm. All parameter values are as provided with the original model at GitHub.
Below, two optimized model files are shared:
-
model_main.xmlhas 9 000 worms on a $1\ \mathrm{cm} \times 1\ \mathrm{cm}$ square, was derived from the authors'worm6c.xmland reproduces the results as published in Figs. S3(C), S3(D) and S3(E) as well as Video S8 in Avery et al.. The published model required 9 days runtime (p.19/25 in Avery et al.) while the optimized model speeds up more than 40 fold to just 5 hours. -
model_full.xmlhas 72 000 worms on a $6\ \mathrm{cm} \times 6\ \mathrm{cm}$ square and was derived from the authors'worm7a.xml. The published model was computationally infeasible to run to completion (p.19/25 in Avery et al.) while the optimized model completes in 2 days on a 16 thread processor.
Results
Published Simulation Results for Small System
 by [Avery _et al._](#reference): Results of model simulation for small system of 9000 worms on a $1\ \mathrm{cm} \times 1\ \mathrm{cm}$ square at time $200.000\ \mathrm{s}$ ([*CC BY 4.0*](https://creativecommons.org/licenses/by/4.0/): [**Avery _et al._**](#reference))](/media/model/m7683/Fig_S3_CDE_hubf6483cabe16ad2808dbf5ff9cf2b519_716026_26c64985e579ccf8f23e7ea9b633bf1f.png)
Reproduced Simulation Results for Small System
: Simulation results of the optimized [`model_main.xml`](/media/model/m7683/model_main.xml) for the small system of 9000 worms on a $1\ \mathrm{cm} \times 1\ \mathrm{cm}$ square at time $200.000\ \mathrm{s}$](/media/model/m7683/Fig_small_system_huc9620a34bfcf21d5375b4c885cb359cd_496164_4780841e6e04f813c1464c95620052ee.png)
model_main.xml for the small system of 9000 worms on a $1\ \mathrm{cm} \times 1\ \mathrm{cm}$ square at time $200.000\ \mathrm{s}$
Video of the simulation of the optimized model_main.xml for the small system of 9000 worms on a $1\ \mathrm{cm} \times 1\ \mathrm{cm}$ square reproduces the dynamics of aggregate formation and fusion as published in Video S8. Numbers at bottom right give time in seconds.
New Simulation Results for Full-scale System
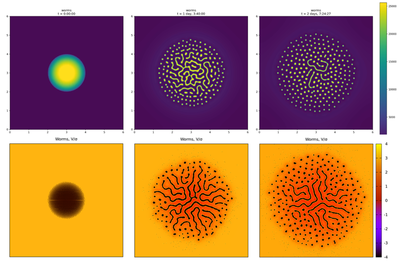
model_full.xml support the published results (top row) of the continuous worm density model as shown in Fig. 6 of Avery et al.. Left column shows initial conditions, middle column the pattern at (around) $100.000\ \mathrm{s}$ and right column the final pattern at (around) $200.000\ \mathrm{s}$. The three panels in the top row were copied from the published Video S6 (CC BY 4.0: Avery et al.). The bottom panels show individual worms as black objects overlayed onto the field $V/\sigma$ according to the color bar at the bottom right.
When 72 000 worms are seeded in the center of a $6\ \mathrm{cm} \times 6\ \mathrm{cm}$ square in the optimized full-scale individual-based model model_full.xml (bottom row in above figure), then round and regularly spaced aggregates are observed in the simulations near the periphery of an expanding disc-shaped area (bottom middle and right in above figure). Individual worms are seen to explore the entire square. Average aggregate size decreases towards the periphery of the disc and aggregates form labyrinth patterns in the high-density center of the disc. These qualitative features agree well with the continuum results (top row in above figure).
Video of the simulation of the optimized model_full.xml for the full-scale system of 72 000 worms on a $6\ \mathrm{cm} \times 6\ \mathrm{cm}$ square. The left panel (Worms, $V/\sigma$) of the first, middle and last time frame ($200\ 000\ \mathrm{s}$) of this video correspond to the bottom row panels in the above figure.
Numbers at bottom right give time in seconds.
To allow detailed inspection of worm shapes and distributions, 21 uncompressed plots of the full-scale simulation every $10\ 000\ \mathrm{s}$ are provided in the attached plots.zip archive.
Reference
This model is the original used in the publication, up to technical updates:
L. Avery, B. Ingalls, C. Dumur, A. Artyukhin: A Keller-Segel model for C elegans L1 aggregation. PLOS Computational Biology 17(7): e1009231, 2021.
Model
model_main.xml
XML Preview
<?xml version='1.0' encoding='UTF-8'?>
<MorpheusModel version="4">
<Description>
<Details>Full title: Caenorhabditis elegans L1 Aggregation
Date: 12.09.2022
Authors: L. Avery, B. Ingalls, C. Dumur, A. Artyukhin
Contributor: L. Brusch
Software: Morpheus (open-source), download from https://morpheus.gitlab.io
Time unit: second
Space unit: cm
ModelID: https://identifiers.org/morpheus/M7683
Comment: Attractant+repellent Keller-Segel model, 1 cm x 1 cm, starting with 9.000 worms uniformly.
This model reproduces results from the following publication in the latest Morpheus version which were originally obtained with the same model in an older Morpheus version.
Reference: L. Avery, B. Ingalls, C. Dumur, A. Artyukhin. "A Keller-Segel model for C elegans L1 aggregation"
PLOS Computational Biology 17(7), e1009231, 2021.
https://doi.org/10.1371/journal.pcbi.1009231
</Details>
<Title>Worm</Title>
</Description>
<Space>
<Lattice class="square">
<Neighborhood>
<Order>1</Order>
</Neighborhood>
<Size symbol="size" value="384, 384, 0"/>
<BoundaryConditions>
<Condition type="periodic" boundary="x"/>
<Condition type="periodic" boundary="y"/>
</BoundaryConditions>
<NodeLength symbol="dx" value="0.0026041666666666665"/>
</Lattice>
<SpaceSymbol symbol="space"/>
</Space>
<Time>
<StartTime value="0"/>
<StopTime symbol="tmax" value="200000"/>
<TimeSymbol symbol="time"/>
<RandomSeed value="123456"/>
</Time>
<Analysis>
<ModelGraph include-tags="#untagged" format="svg" reduced="false"/>
<Function symbol="Va">
<Expression>-beta_a*log(alpha_a + Ua)</Expression>
</Function>
<Function symbol="Vaos2">
<Expression>Va + beta_a*log(alpha_a)</Expression>
</Function>
<Function symbol="Vr">
<Expression>-beta_r*log(alpha_r + Ur)</Expression>
</Function>
<Function symbol="Vros2">
<Expression>Vr+beta_r*log(alpha_r+Ur)</Expression>
</Function>
<Function symbol="Vos2">
<Expression>Vaos2+Vros2</Expression>
</Function>
<Gnuplotter time-step="treport" name="fields" decorate="true" file-numbering="time">
<Plot title="Worms, V/σ">
<!-- <Disabled>
<Cells value="cell.clusterID"/>
</Disabled>
-->
<Cells value="cell.type"/>
<Field symbol-ref="V" max="4" min="-3"/>
</Plot>
<Terminal name="png" size="2000,1000,0"/>
<Plot>
<Field symbol-ref="Ua" max="30000" min="0"/>
</Plot>
<Plot>
<Field symbol-ref="Ur" max="9000" min="5000"/>
</Plot>
</Gnuplotter>
<Gnuplotter time-step="treport" name="Vplot" decorate="true" file-numbering="time">
<Plot>
<Field symbol-ref="V"/>
</Plot>
<Terminal name="png" size="2000,2000,0"/>
<Plot>
<Field symbol-ref="Va"/>
</Plot>
<Plot>
<Field symbol-ref="Vr"/>
</Plot>
</Gnuplotter>
<Logger time-step="treport">
<Input>
<Symbol symbol-ref="cell.id"/>
<Symbol symbol-ref="cell.center.x"/>
<Symbol symbol-ref="cell.center.y"/>
<Symbol symbol-ref="delta_r.x"/>
<Symbol symbol-ref="delta_r.y"/>
<Symbol symbol-ref="MKtemp"/>
<Symbol symbol-ref="MKtime"/>
<Symbol symbol-ref="cmstrength"/>
</Input>
<Output>
<TextOutput file-name="worms" file-format="csv" header="true" separator="comma" file-numbering="time"/>
</Output>
</Logger>
<Logger time-step="treport">
<Input>
<Symbol symbol-ref="space.x"/>
<Symbol symbol-ref="space.y"/>
<Symbol symbol-ref="Ua"/>
<Symbol symbol-ref="Va"/>
<Symbol symbol-ref="Ur"/>
<Symbol symbol-ref="Vr"/>
<Symbol symbol-ref="V"/>
</Input>
<Output>
<TextOutput file-name="UaUr" file-format="csv" header="true" separator="comma" file-numbering="time"/>
</Output>
</Logger>
<ClusteringTracker celltype="medium,worm" time-step="treport" exclude="cell.type==celltype.medium.id" name="Cluster size distribution">
<ClusterID symbol-ref="cell.clusterID"/>
</ClusteringTracker>
</Analysis>
<CPM>
<Interaction>
<Contact type2="worm" type1="worm" value="wormtoworm"/>
<Contact type2="medium" type1="worm" value="wormtomedium"/>
</Interaction>
<ShapeSurface scaling="norm">
<Neighborhood>
<Order>1</Order>
</Neighborhood>
</ShapeSurface>
<MonteCarloSampler stepper="edgelist">
<MCSDuration symbol="MKtime" value="0.15"/>
<MetropolisKinetics temperature="MKtemp"/>
<Neighborhood>
<Order>1</Order>
</Neighborhood>
</MonteCarloSampler>
</CPM>
<CellTypes>
<CellType name="worm" class="biological">
<ConnectivityConstraint/>
<VolumeConstraint target="cellvolume" strength="1"/>
<MotilityReporter time-step="1000" name="worm_motility">
<Displacement symbol-ref="delta_r"/>
<Velocity symbol-ref="vel"/>
</MotilityReporter>
<PropertyVector symbol="vel" value="0.0, 0.0, 0.0"/>
<PropertyVector symbol="delta_r" value="0.0, 0.0, 0.0"/>
<Chemotaxis strength="cmstrength" field="-V"/>
<Property symbol="gridsa" value="sa/wormvolume"/>
<Property symbol="gridsr" value="sr/wormvolume"/>
<Property symbol="cell.clusterID" value="0"/>
</CellType>
<CellType name="medium" class="medium">
<PropertyVector symbol="delta_r" value="0.0, 0.0, 0.0"/>
<PropertyVector symbol="vel" value="0.0, 0.0, 0.0"/>
<Property symbol="gridsa" value="0"/>
<Property symbol="gridsr" value="0.0"/>
<Property symbol="cell.clusterID" value="-1"/>
</CellType>
</CellTypes>
<CellPopulations>
<Population type="worm" size="360">
<InitRectangle mode="random" number-of-cells="Nworms">
<Dimensions origin="0.0, 0.0, 0.0" size="size.x, size.y, size.z"/>
</InitRectangle>
</Population>
</CellPopulations>
<Global>
<Constant symbol="treport" value="1000"/>
<Constant symbol="width" name="width" value="size.x*dx"/>
<Constant symbol="dt" value="MKtime"/>
<Constant symbol="nelements" name="nelements" value="size.x"/>
<Constant symbol="sweep" name="sweep" value="1"/>
<Constant symbol="MKtemp" value="10.0"/>
<Field symbol="Ua" name="Attractant" value="0.0">
<Diffusion rate="1e-6"/>
</Field>
<Field symbol="Ur" name="Repellent" value="0.0">
<Diffusion rate="1e-5"/>
</Field>
<Field symbol="V" name="Combined potential" value="0.0"/>
<Constant symbol="mu" value="MKtemp"/>
<Constant symbol="cmstrength" value="mu"/>
<Constant symbol="wormtoworm" value="0.0"/>
<Constant symbol="wormtomedium" value="0.0"/>
<Constant symbol="cellvolume" value="5"/>
<Constant symbol="wormvolume" value="cellvolume*dx*dx"/>
<Constant symbol="rho_bar" value="9000"/>
<Constant symbol="Nworms" value="width*width*rho_bar"/>
<ConstantVector symbol="delta_r" value="0.0, 0.0, 0.0"/>
<ConstantVector symbol="vel" value="0.0, 0.0, 0.0"/>
<Constant symbol="sa" value="0.01"/>
<Constant symbol="s2" value="5.55555e-6"/>
<Constant symbol="alpha_a" value="1500"/>
<Constant symbol="beta_a" value="2"/>
<Constant symbol="sr" value="0.001"/>
<Constant symbol="alpha_r" value="1500"/>
<Constant symbol="beta_r" value="-2"/>
<System time-step="1" name="Dynamics dt=1 RK(4)" solver="Runge-Kutta [fixed, O(4)]">
<DiffEqn symbol-ref="Ua">
<Expression>gridsa - gamma_a*Ua</Expression>
</DiffEqn>
<Constant symbol="gamma_a" value="0.01"/>
<DiffEqn symbol-ref="Ur">
<Expression>gridsr-gamma_r*Ur</Expression>
</DiffEqn>
<Constant symbol="gamma_r" value="0.001"/>
<Rule symbol-ref="V">
<Expression>-beta_a*log(alpha_a + Ua)-beta_r*log(alpha_r + Ur)</Expression>
</Rule>
</System>
</Global>
</MorpheusModel>

Downloads
Files associated with this model: