Hold cell in place
Persistent Identifier
Use this permanent link to cite or share this Morpheus model:
Can a CPM cell be held in a defined position and continue its other dynamics?
Introduction
CPM cells inherently interact with other cells by volume exclusion (steric interaction) and can get pushed out of the way. Here, we compare three cell behaviors where, in addition to steric interactions, either a cell’s center of mass or the entire cell shape get fixed. All other dynamics continue inside each cell and on each cell shape. This example was motivated by Ivan in the Morpheus user forum.
Model Description
This model has two CellTypes. The first, our cells of interest, is used to initialize 3 cells in a column. All model elements that control aspects of the cell shape are tagged with cell. Just to demonstrate that all other dynamics continue inside each cell, on its membrane and in its interaction with a global field, we also let these cells perform intracellular and membrane dynamics (tagged membrane) that interact with an extracellular field (tagged global).
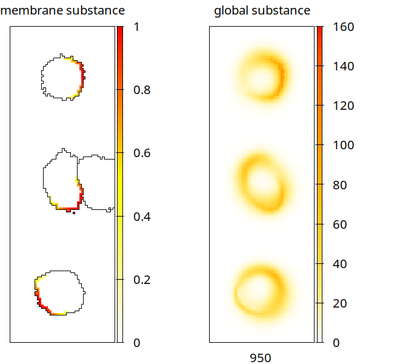
The second CellTypes gives a single runner cell on the right lane that just aims to perturb the three other cells.
Results
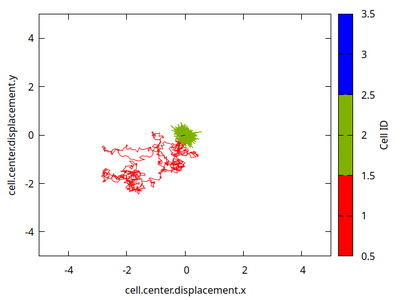
Based on the cells' IDs, we let cell ID=1 (bottom cell in column and red trajectory in following plot) perform the normal membrane fluctuations of a CPM. Its center of mass fluctuates strongly and gets pushed away 3 lattice units (within the shown 1000 MCS) from its initial position.
The cell with ID=2 (middle and green trajectory) stores the initial position of its center of mass and uses DirectedMotion in opposite direction from its displacement to restore that position after a perturbation. This yields minute fluctuations of less than a lattice unit. The strength parameter of DirectedMotion allows to tune the rigidity of the center of mass position. The cell shape remains flexible.
The cell with ID=3 (top and blue trajectory) freezes its entire shape after an initial time step (the condition to freeze after one time step is chosen such that a short line becomes visible in the trajectory plot).
The runner cell then squeezes around the frozen cell, reversibly deforms the middle cell (that is held in place) and it pushes aside the normal bottom cell.
We can also record the history of lattice nodes that once were occupied by the membranes of cells 1, 2, 3 (see following plots). The runner cell was excluded here.
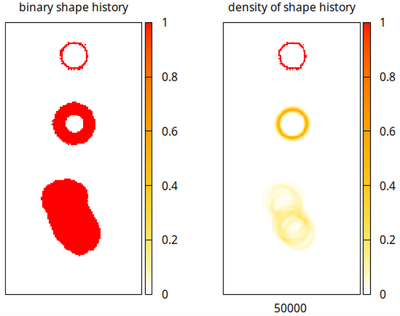
The same method may also be used to force cells along arbitrary (microscopy image-derived) trajectories by inserting data into the calculation of the displacement vector.
Model
model.xml
XML Preview
<?xml version='1.0' encoding='UTF-8'?>
<MorpheusModel version="4">
<Description>
<Details>Full title: Hold cell in place
Authors: J. Starruß
Contributors: L. Brusch
Date: 21.10.2024
Software: Morpheus (open-source). Download from https://morpheus.gitlab.io
Model ID: https://identifiers.org/morpheus/M5495
</Details>
<Title>Hold cell</Title>
</Description>
<Space>
<Lattice class="square">
<Neighborhood>
<Order>1</Order>
</Neighborhood>
<Size symbol="size" value="50, 150, 0"/>
<BoundaryConditions>
<Condition type="noflux" boundary="x"/>
<Condition type="noflux" boundary="-x"/>
<Condition type="periodic" boundary="y"/>
<Condition type="periodic" boundary="-y"/>
</BoundaryConditions>
</Lattice>
<SpaceSymbol symbol="space"/>
<MembraneLattice>
<Resolution symbol="memsize" value="100"/>
<SpaceSymbol symbol="memspace"/>
<Annotation>MembraneLattice resolution is defined here. In CellType, this then allows to use dynamics of spatial fields on the membrane of CPM cells. Please see the InApp-Docu for more details on MembraneLattice.</Annotation>
</MembraneLattice>
</Space>
<Time>
<StartTime value="0"/>
<StopTime value="1000"/>
<TimeSymbol symbol="time"/>
</Time>
<CellTypes>
<CellType name="cell" class="biological">
<VolumeConstraint target="400" strength="1" tags="cell"/>
<SurfaceConstraint target="1" strength="1" mode="aspherity" tags="cell"/>
<MembraneProperty symbol="m" name="membrane substance" tags="membrane" value="sin(angle_secretion-memspace.phi) * (sin(angle_secretion-memspace.phi)>0)">
<Diffusion rate="0.0"/>
<Annotation>Just for demonstration purposes, this MembraneProperty is controlling the directed secretion of the substanc.</Annotation>
</MembraneProperty>
<PropertyVector symbol="cell.center.initial" tags="cell" value="cell.center"/>
<PropertyVector symbol="cell.center.displacement" tags="cell" value="0.0, 0.0, 0.0"/>
<VectorEquation symbol-ref="cell.center.displacement" tags="cell">
<Expression>cell.center - cell.center.initial</Expression>
</VectorEquation>
<DirectedMotion strength="1*(cell.id==2)" direction="- cell.center.displacement" tags="cell"/>
<FreezeMotion tags="cell">
<Condition>(time>0)*(cell.id==3)</Condition>
</FreezeMotion>
<Property symbol="angle_secretion" tags="membrane" value="0.0"/>
<System time-step="100" name="Demo intracellular dynamics" solver="Euler [fixed, O(1)]" tags="membrane">
<Rule symbol-ref="angle_secretion">
<Expression>rand_uni(0,2*pi)</Expression>
</Rule>
</System>
<System time-step="100" name="Demo membrane dynamics on cell shape" solver="Euler [fixed, O(1)]" tags="membrane">
<Rule symbol-ref="m">
<Expression>sin(angle_secretion-memspace.phi) * (sin(angle_secretion-memspace.phi)>0)</Expression>
</Rule>
</System>
</CellType>
<CellType name="runner" class="biological">
<VolumeConstraint target="400" strength="1" tags="cell"/>
<SurfaceConstraint target="1" strength="1" mode="aspherity" tags="cell"/>
<DirectedMotion strength="1" direction="0,-1,0" tags="cell"/>
</CellType>
</CellTypes>
<CPM>
<Interaction/>
<ShapeSurface scaling="norm">
<Neighborhood>
<Order>optimal</Order>
</Neighborhood>
</ShapeSurface>
<MonteCarloSampler stepper="edgelist">
<MCSDuration value="1"/>
<MetropolisKinetics temperature="1"/>
<Neighborhood>
<Order>optimal</Order>
</Neighborhood>
</MonteCarloSampler>
</CPM>
<CellPopulations>
<Population type="cell" size="0">
<InitCellObjects mode="distance" tags="cell">
<Arrangement repetitions="1, 3, 1" displacements="0, 50, 0">
<Sphere center="25,25,0" radius="10"/>
</Arrangement>
</InitCellObjects>
</Population>
<Population type="runner" size="1">
<InitCellObjects mode="distance" tags="cell">
<Arrangement repetitions="1, 1, 1" displacements="0, 0, 0">
<Sphere center="37,100,0" radius="10"/>
</Arrangement>
</InitCellObjects>
</Population>
</CellPopulations>
<Analysis>
<Gnuplotter time-step="10">
<Terminal name="png"/>
<Plot>
<Cells value="m">
<ColorMap>
<Color color="red" value="2"/>
<Color color="yellow" value="1"/>
<Color color="white" value="0"/>
</ColorMap>
</Cells>
</Plot>
<Plot>
<Field symbol-ref="c" max="160" min="0"/>
</Plot>
</Gnuplotter>
<ModelGraph include-tags="#untagged,global,membrane,cell" format="dot" reduced="false"/>
<Logger time-step="1.0">
<Input/>
<Output>
<TextOutput file-separation="cell"/>
</Output>
<Plots>
<Plot time-step="-1">
<Style style="lines"/>
<Terminal terminal="png"/>
<X-axis minimum="-5" maximum="5">
<Symbol symbol-ref="cell.center.displacement.x"/>
</X-axis>
<Y-axis minimum="-5" maximum="5">
<Symbol symbol-ref="cell.center.displacement.y"/>
</Y-axis>
<Color-bar>
<Symbol symbol-ref="cell.id"/>
</Color-bar>
</Plot>
</Plots>
<Restriction>
<Celltype celltype="cell"/>
</Restriction>
</Logger>
</Analysis>
<Global>
<Field symbol="c" name="global substance" tags="global" value="0">
<Diffusion rate="0.01"/>
<Annotation>Global Field for secreted substance. This field is initialized as 0 and will then "take up" the substance that is secreted by the cells.</Annotation>
</Field>
<Constant symbol="m" name="membrane substance" tags="membrane" value="0">
<Annotation>We need to introduce another constant for the substance in the Global scope wherever it is not reset by the value of the membrane field with the same Symbol (with its dynamics defined in the Cell scope).</Annotation>
</Constant>
<System time-step="1.0" name="Secretion System" solver="Runge-Kutta [fixed, O(4)]" tags="membrane, global">
<DiffEqn symbol-ref="c">
<Expression>m - 0.001*c</Expression>
</DiffEqn>
</System>
</Global>
</MorpheusModel>

Downloads
Files associated with this model: