Eukaryotic Cell Motility Based on Actin Waves on the Cell Edge

J. Algorta, A. Fele-Paranj, J. M. Hughes, L. Edelstein-Keshet (Authors)
J. Algorta, L. Edelstein-Keshet (Contributors)
Persistent Identifier

Use this permanent link to cite or share this Morpheus model:

Cell motility simulation with a reaction-diffusion model for actin waves on the cell perimeter

Introduction

A partial differential equation model for ‘actin waves’ by Holmes et al., 2012 was simplified and investigated by PDE bifurcation analysis in Hughes et al., 2024.

This model is related to our model of actin waves in 1D and our previous work Mata et al., 2013 and Liu et al., 2021.

Description

The model accounts for active ($u$) and inactive ($v$) GTPase (such as Rac) and its nucleation of filamentous actin ($F$). We assumed that Rac promotes F-actin assembly, and that F-actin contributes negative feedback (inactivation of Rac).

The model equations are:

$$\begin{align} \frac{\partial u}{\partial t} &= (b+\gamma u^2)v - (1+sF+u^2)u + D \Delta u \\ \frac{\partial v}{\partial t} &= -(b+\gamma u^2)v + (1+sF+u^2)u + \Delta v \\ \frac{\partial F}{\partial t} &= \epsilon (p_0+p_1 u - F) + D_F \Delta F \end{align}$$

The dynamics of these equations in a 1D periodic domain, and XML files for simulating the model are given on model page M2071.

Here we investigate the effect of ‘actin wave’ dynamics on the protrusion and motility of a eukaryotic cell.

We assumed that the reaction-diffusion model operates on the 1D periodic cell-edge domain of a CPM cell. Using the Morpheus plugin StarConvex membrane based on the level of F-actin ($F$), we simulated the PDEs as a MembraneProperty system for a single cell, with parameter values given in the table below.

Polar Cell Turning Cell
Parameters $b$ $0.067$ $0.00067$
$\gamma$ $3.55$ $3$
$s$ $0.41$ $1$
$\epsilon$ $0.6$ $0.6$
$p_0$ $0.8$ $0.8$
$p_1$ $3.8$ $3.8$
$D$ $0.1$ $0.1$
$D_F$ $0.001$ $0.001$
 lengthscale $\frac{1}{5}$ $\frac{1}{100}$
Model file Polar_Cell_
Motility_main.xml		 Turning_Cell_
Motility.xml
Table 1: Parameter values for the Polar Cell and Turning Cell configurations. For the two-lobe (Two_Lobe_Cell.xml) and three-lobe (Three_Lobe_Cell.xml) configurations, the lengthscale parameter is set as described below, and all other parameters are as for the Turning Cell configuration.

To observe distinct behaviors, we picked cells of ‘different sizes’: we used similar kinetic parameters, but changed the lengthscale.

The lengthscale was obtained by adjusting the diffusion coefficients: in the Polar Cell, this coefficient was set to $\frac{1}{5}$; in the Turning Cell, to $\frac{1}{100}$; in the two-lobe configuration, to $\frac{1}{50}$ (twice the Turning Cell coefficient); and in the three-lobe configuration, to $\frac{1}{33}$ (three times the Turning Cell coefficient).

Results

Cell shape and motility vary depending on the type of PDE solution, determined by the parameter values and domain size, $L$. Four qualitatively different motility states are compared in Figure 1 (a)-(d) and the associated Videos 1-4 below. For each case, the corresponding model file is linked in the video caption.

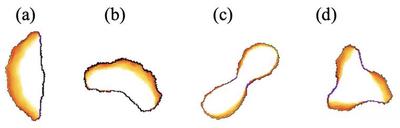
Figure 1: **(a)** Polar cell, **(b)** turning cell, **(c)** two-lobe cell, **(d)** three-lobe cell. The latter two are less motile than the first two.
Figure 1: (a) Polar cell, (b) turning cell, (c) two-lobe cell, (d) three-lobe cell. The latter two are less motile than the first two.
Video 1. A single stable polarization along the cell edge yields straight cell motility, corresponding to Figure 1(a) and Polar_Cell_Motility_main.xml
Video 2. A single traveling polarization along the cell edge yields cell turning, corresponding to Figure 1(b) and Turning_Cell_Motility.xml
Video 3. Two periods of polarization along the cell edge yield a two-lobed cell which may also be turning, corresponding to Figure 1(c) and Two_Lobe_Cell.xml
Video 4. Three or more periods of polarization along the cell edge yield a three-lobed cell or a four-lobed cell that may also be turning, corresponding to Figure 1(d) and Three_Lobe_Cell.xml

Reference

This model is the original used in the publication, up to technical updates:

J. Algorta, A. Fele-Paranj, J. M. Hughes, L. Edelstein-Keshet: Modeling and Simulating Single and Collective Cell Motility. Cold Spring Harbour Perspectives in Biology, 2024.

Model

Get this model via:

  • Morpheus-Link or
  •  Download: Polar_Cell_Motility_main.xml

    • XML Preview 

    <MorpheusModel version="4">
    <Description>
        <Title>M2072: Polar Cell Motility</Title>
        <Details>Model ID:	https://identifiers.org/morpheus/M2072
  File type:	Main model
  Software:	Morpheus (open source). Download from: https://morpheus.gitlab.io
Full title:	Eukaryotic Cell Motility – Polar Cell 
Authors:	J. Algorta, A. Fele-Paranj, J. M. Hughes, L. Edelstein-Keshet
Submitter:	J. Algorta, L. Edelstein-Keshet
Curator:	D. Jahn
Date:	12.11.2024
Reference:	J. Algorta, A. Fele-Paranj, J. M. Hughes, L. Edelstein-Keshet: Modeling and Simulating Single and Collective Cell Motility. Cold Spring Harbour Perspectives in Biology, 2024.
	This model is the original used in Figure 2 of the publication, up to technical updates.
Comment:	PDE model for F-actin negative feedback to GTPases, and GTPase promotion of F-actin. The reaction-diffusion PDEs are implemented on the cell edge.
	u = active GTPase (Rac)
	v = inactive GTPase
	F = F-actin</Details>
    </Description>
    <Global>
        <Constant symbol="lengthscale" value="1/5"/>
        <Field symbol="prot" value="0.0"/>
    </Global>
    <Space>
        <Lattice class="square">
            <Size symbol="lattice" value="600, 600, 0"/>
            <BoundaryConditions>
                <Condition type="periodic" boundary="x"/>
                <Condition type="periodic" boundary="y"/>
            </BoundaryConditions>
            <NodeLength value="1.0"/>
            <Neighborhood>
                <Distance>2.0</Distance>
            </Neighborhood>
        </Lattice>
        <SpaceSymbol symbol="l"/>
        <MembraneLattice>
            <Resolution symbol="memsize" value="1500"/>
            <SpaceSymbol symbol="m"/>
        </MembraneLattice>
    </Space>
    <Time>
        <StartTime value="0"/>
        <StopTime value="400"/>
        <SaveInterval value="0"/>
        <!--    <Disabled>
        <RandomSeed value="0"/>
    </Disabled>
-->
        <TimeSymbol symbol="time"/>
    </Time>
    <CellTypes>
        <CellType class="biological" name="cells">
            <VolumeConstraint target="4800" strength="1"/>
            <SurfaceConstraint target="1.2" strength="1" mode="aspherity"/>
            <MembraneProperty symbol="u" name="Active form of protein" value="1-0.5*cos(m.phi)">
                <Diffusion rate="0.1/lengthscale^2"/>
            </MembraneProperty>
            <MembraneProperty symbol="v" name="Inactive form of protein" value="1-0.1*cos(m.phi)">
                <Diffusion rate="1/lengthscale^2"/>
            </MembraneProperty>
            <MembraneProperty symbol="F" name="F-actin" value="4.5-0.82*cos(m.phi)">
                <Diffusion rate="0.001/lengthscale^2"/>
            </MembraneProperty>
            <Constant symbol="T" value="0"/>
            <System time-step="0.05" name="WavePinning with Inhibitor" time-scaling="0.1" solver="Runge-Kutta [fixed, O(4)]">
                <Constant symbol="b" value="0.067"/>
                <Constant symbol="gamma" value="3.55"/>
                <Constant symbol="s" value="0.41"/>
                <Constant symbol="eps" value="0.6"/>
                <Constant symbol="p0" value="0.8"/>
                <Constant symbol="p1" value="3.8"/>
                <Intermediate symbol="A" value="(b+gamma*u^2)*v-(1+(s)*F+(1+trial*T)*u^2)*u"/>
                <DiffEqn symbol-ref="u">
                    <Expression>A</Expression>
                </DiffEqn>
                <DiffEqn symbol-ref="v">
                    <Expression>-A</Expression>
                </DiffEqn>
                <DiffEqn symbol-ref="F">
                    <Expression>eps*(p0+p1*u-F)</Expression>
                </DiffEqn>
                <Constant symbol="trial" value="0"/>
            </System>
            <StarConvex retraction="false" membrane="F" protrusion="true" strength="5"/>
            <Protrusion maximum="150" strength="10.5" field="prot"/>
        </CellType>
    </CellTypes>
    <CPM>
        <Interaction default="0.0"/>
        <MonteCarloSampler stepper="edgelist">
            <MCSDuration value="0.01"/>
            <Neighborhood>
                <Order>2</Order>
            </Neighborhood>
            <MetropolisKinetics yield="0.05" temperature="1"/>
        </MonteCarloSampler>
        <ShapeSurface scaling="norm">
            <Neighborhood>
                <Order>6</Order>
            </Neighborhood>
        </ShapeSurface>
    </CPM>
    <CellPopulations>
        <Population type="cells" size="0">
            <InitCellObjects mode="distance">
                <Arrangement displacements="1, 1, 0" repetitions="1, 1, 0">
                    <Sphere radius="24*2" center="400 200 0"/>
                </Arrangement>
            </InitCellObjects>
        </Population>
    </CellPopulations>
    <Analysis>
        <Logger time-step="10">
            <Input>
                <Symbol symbol-ref="m.phi"/>
                <Symbol symbol-ref="u"/>
                <Symbol symbol-ref="T"/>
                <Symbol symbol-ref="F"/>
            </Input>
            <Output>
                <TextOutput/>
            </Output>
            <Plots>
                <Plot time-step="10">
                    <Style style="points"/>
                    <Terminal terminal="png"/>
                    <X-axis maximum="6.28">
                        <Symbol symbol-ref="m.phi"/>
                    </X-axis>
                    <Y-axis maximum="10">
                        <Symbol symbol-ref="u"/>
                        <Symbol symbol-ref="v"/>
                        <Symbol symbol-ref="F"/>
                    </Y-axis>
                    <Range>
                        <Time mode="current"/>
                    </Range>
                </Plot>
            </Plots>
        </Logger>
        <ModelGraph format="dot" reduced="false" include-tags="#untagged"/>
        <Gnuplotter time-step="5" decorate="false">
            <Plot>
                <Cells value="F"/>
                <Field symbol-ref="prot"/>
            </Plot>
            <Terminal name="png" size="1200,1200,0"/>
            <!--    <Disabled>
        <Plot/>
    </Disabled>
-->
        </Gnuplotter>
    </Analysis>
</MorpheusModel>

    Model Graph
    Model Graph

    Downloads

    Files associated with this model:

    2D Actin Actin Wave Actin Wave Dynamics Cell Edge Cell Motility Cell Shape Cellular Potts Model CPM Deterministic Model Dictyostelium Discoideum Diffusion Eukaryotic Cell F-actin Filamentous Actin GTPase Lobed Cell Lobed-cell Motility Membrane MembraneProperty Microorganisms Motility Multi-Lobed Cell Negative Feedback Partial Differential Equation PDE Polar Cell Polarity Polarization Protrusion Published Models Rac Reaction-diffusion System Single-Cell Spatial Model StarConvex Three-Lobe Cell Turning Cell Two-Lobe Cell Wave Dynamics
    Next

    Last updated on Fri, 20 Dec 2024

    Related