Two Layer Circuit
Persistent Identifier
Use this permanent link to cite or share this Morpheus model:
Introduction
This model combines simple Notch signaling with the cellular Potts model (CPM), which drives cell sorting as a result of differential adhesion. Model details are contained in the reference Mulberry and Keshet, 2020.
In this experiment, we consider a mixture of two distinct genotypes (a sender cell and a receiver cell), which become ‘activated’ and eventually self-organize into a stable two-layer structure.
Description
We define two cell types. Cell type A are the so-called sender cells, which produce the ligand Delta. Cell type B are the receiver cells, which produce the Notch receptor. A-type cells activate neighbouring B cells, thereby inducing the B cells to produce an E-cadherin protein. This promotes adhesion among activated B cells.
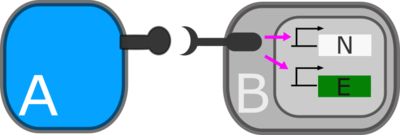
The equation for ligand $D$ expressed by A-type sender cells is $$ \frac{\mathrm dD}{\mathrm dt} = D_0 - \kappa_tN_\text{ext}D - \gamma D$$
Here $D$, produced at a constant rate $D_0$, is used up in binding to neighboring receiver Notch receptors $N_\text{ext}$, and has some inherent rate of decay.
The B-type receiver cells have Notch receptors $N$ that get activated by sender ligand $D_\text{ext}$. Upon activation, the Notch receptor releases its intracellular domain ($I$), which then activates gene expression and production of E-cad ($E$). Model equations for a receiver cell are:
$$\begin{align} \frac{\mathrm dN}{\mathrm dt} &= N_0 \left(1 + \frac{I^p}{I_0^p+I^p}\right) - \kappa_tND_\text{ext}-\gamma N \\ \frac{\mathrm dI}{\mathrm dt} &= \kappa_tND_\text{ext}- \gamma_I I\\ \frac{\mathrm dE}{\mathrm dt} &= E_0 \frac{I^p}{I_0^p+I^p} - \gamma E\\ \end{align}$$
The ligand $D_\text{ext}$ of B neighbors trans-activates Notch at rate $\kappa_t$. Protein degradation occurs at rate $\gamma$ for Notch and E-cad, and at rate $\gamma I$ for $I$.
Results
In most computational experiments, we observe that the cells are able to self-organize into a two layer structure within $T = 200$ hours. Once sorted, the cells retain their ‘sender’ and ‘receiver’ characteristics, but we avoid any mechanism for irreversible cell-fate determination. Hence, the spatial distribution of the cells influences their dynamic interactions. We observe in simulations that, over longer time frames, the inner core of green cells starts to deactivate, and subsequently migrate outwards. However, once these deactivated cells reach the boundary of this core, they can once again become activated. This illustrates the stability of the two layer structure.

Reference
This model is described in the peer-reviewed publication:
N. Mulberry, L. Edelstein-Keshet: Self-organized Multicellular Structures from Simple Cell Signaling: A Computational Model. Phys. Biol. 17: 066003, 2020.
Our computational model was inspired by the experimental work of Toda et al., 2018. The Notch signaling model was based on that of Boareto et al., 2015.
Model
TwoLayerCircuit.xml
XML Preview
<MorpheusModel version="4">
<Description>
<Title>Two Layer Circuit</Title>
<Details>
Two distinct cell types: a sender cell A and a receiver cell B.
The B-type cells are induced by A to express E-cadherin, which leads to
cell sorting. For certain parameter values, a two-layer structure
emerges. Blue colour indicates the A-type cells, and green colour indicates
differentiated B-type cells.
Reference:
The model is decribed in "Self-organized multicellular structures from simple cell signaling: a computational model",
N.Mulberry and L.Edelstein-Keshet, Physical Biology 2020, https://doi.org/10.1088/1478-3975/abb2dc
</Details>
</Description>
<Global>
<Variable symbol="N" value="0"/>
<Variable symbol="D" value="0"/>
<Variable symbol="I" value="0"/>
<Variable symbol="E" value="0"/>
<Variable symbol="colour" value="0"/>
</Global>
<Space>
<SpaceSymbol symbol="l"/>
<Lattice class="square">
<Size symbol="size" value="300, 300, 0"/>
<BoundaryConditions>
<Condition boundary="x" type="noflux"/>
<Condition boundary="y" type="noflux"/>
</BoundaryConditions>
<Neighborhood>
<Order>1</Order>
</Neighborhood>
</Lattice>
</Space>
<Time>
<StartTime value="0"/>
<StopTime value="2e2"/>
<TimeSymbol symbol="time"/>
</Time>
<CellTypes>
<!-- A type cells: the "sender" cells, hiD loN -->
<CellType class="biological" name="A">
<VolumeConstraint target="200" strength="1"/>
<Property symbol="N" value="0.0" name="notch"/>
<Property symbol="Nn" value="0.0" name="notch_Neighbours"/>
<Property symbol="D" value="3e3" name="delta"/>
<Property symbol="Dn" value="0.0" name="delta_Neighbours"/>
<Property symbol="I" value="0.0" name="NICD"/>
<Property symbol="E" value="0.0" name="Ecad" />
<Property symbol="colour" value="-1.0" />
<NeighborhoodReporter>
<Input scaling="cell" value="N"/>
<Output symbol-ref="Nn" mapping="average"/>
</NeighborhoodReporter>
<NeighborhoodReporter>
<Input scaling="cell" value="D"/>
<Output symbol-ref="Dn" mapping="average"/>
</NeighborhoodReporter>
<System solver="runge-kutta" time-step="0.1" time-scaling="1">
<Constant symbol="Kt" value="5e-5"/>
<Constant symbol="D0" value="1000"/>
<Constant symbol="gamma" value="0.1"/>
<Constant symbol="p" value="2"/>
<DiffEqn symbol-ref="D">
<Expression> D0 - Kt*D*Nn - gamma*D</Expression>
</DiffEqn>
</System>
</CellType>
<!-- B type cells: the "reciever" cells, loD hiN (express Ecad) -->
<CellType class="biological" name="B">
<VolumeConstraint target="200" strength="1"/>
<Property symbol="N" value="1e3" name="notch"/>
<Property symbol="Nn" value="0.0" name="notch_Neighbours"/>
<Property symbol="D" value="0.0" name="delta"/>
<Property symbol="Dn" value="0.0" name="delta_Neighbours"/>
<Property symbol="I" value="0.0" name="NICD"/>
<Property symbol="E" value="0" name="Ecad" />
<Property symbol="colour" value="0.0" />
<NeighborhoodReporter>
<Input scaling="cell" value="N"/>
<Output symbol-ref="Nn" mapping="average"/>
</NeighborhoodReporter>
<NeighborhoodReporter>
<Input scaling="cell" value="D"/>
<Output symbol-ref="Dn" mapping="average"/>
</NeighborhoodReporter>
<System solver="runge-kutta" time-step="0.1" time-scaling="1">
<Constant symbol="Kt" value="5e-5"/>
<Constant symbol="N0" value="500"/>
<Constant symbol="I0" value="200"/>
<Constant symbol="gammaI" value="0.5"/>
<Constant symbol="gamma" value="0.1"/>
<Constant symbol="p" value="2"/>
<DiffEqn symbol-ref="N">
<Expression>N0*(1+I^p/(I0^p+I^p)) - Kt*N*Dn - gamma*N</Expression>
</DiffEqn>
<DiffEqn symbol-ref="I">
<Expression>Kt*N*Dn - gammaI*I </Expression>
</DiffEqn>
<DiffEqn symbol-ref="E">
<Expression> (I^p/(I0^p+I^p) - gamma*E) </Expression>
</DiffEqn>
<Rule symbol-ref="colour">
<Expression>E/10</Expression>
</Rule>
</System>
</CellType>
<CellType class="medium" name="medium"/>
</CellTypes>
<CPM>
<Interaction>
<Contact type1="A" type2="A" value="16.0"/>
<Contact type1="A" type2="medium" value="22.0"/>
<Contact type1="B" type2="medium" value="22.0"/>
<Contact type1="A" type2="B" value="16.0"/>
<Contact type1="B" type2="B" value="16.0">
<HomophilicAdhesion strength="-1.6" adhesive="E"/>
</Contact>
</Interaction>
<MonteCarloSampler stepper="edgelist">
<!-- cells should be sorted within 24 hrs -->
<MCSDuration value="0.001"/>
<Neighborhood>
<Order>2</Order>
</Neighborhood>
<MetropolisKinetics temperature="10"/>
</MonteCarloSampler>
<ShapeSurface scaling="norm">
<Neighborhood>
<Order>6</Order>
</Neighborhood>
</ShapeSurface>
</CPM>
<CellPopulations>
<Population size="0" type="A">
<InitCircle mode="random" number-of-cells="60">
<Dimensions radius="size.x/3" center="size.x/2, size.y/2, 0"/>
</InitCircle>
</Population>
<Population size="0" type="B">
<InitCircle mode="random" number-of-cells="40">
<Dimensions radius="size.x/3" center="size.x/2, size.y/2, 0"/>
</InitCircle>
</Population>
</CellPopulations>
<Analysis>
<Logger time-step="1">
<Input>
<Symbol symbol-ref="D"/>
<Symbol symbol-ref="N"/>
<Symbol symbol-ref="I"/>
<Symbol symbol-ref="E"/>
<Symbol symbol-ref="cell.type"/>
<Symbol symbol-ref="cell.center.x"/>
<Symbol symbol-ref="cell.center.y"/>
<Symbol symbol-ref="Dn"/>
</Input>
<Output>
<TextOutput/>
</Output>
</Logger>
<Gnuplotter time-step="1" decorate="false">
<Terminal size="800 400 0" persist="true" name="png"/>
<Plot>
<Cells value="colour" min="-1" max="1">
<ColorMap>
<Color value="-1" color="blue"/>
<Color value="0.0" color="grey"/>
<Color value="1.0" color="green"/>
</ColorMap>
</Cells>
</Plot>
</Gnuplotter>
</Analysis>
</MorpheusModel>
Downloads
Files associated with this model: