Drosophila Wing Primordium

J. M. Osborne, A. G. Fletcher, J. M. Pitt-Francis, P. K. Maini, D. J. Gavaghan (Authors)

H. J. Wiederanders, P. H. Suhrcke, P. Rossbach (Contributors)

Persistent Identifier

Use this permanent link to cite or share this Morpheus model:

How does morphogen transport in a growing tissue feed back on tissue growth through morphogen signaling and cell division?

Introduction

The Drosophila wing primordium is a two-dimensional epithelial tissue that grows in response to the concentration profile of the morphogen Dpp (see Fig.1). Dpp molecules get synthesized within a narrow (here vertical) stripe and are transported at least partly by the cells: (i) through cycles of endocytosis and exocytosis and/or (ii) by transient binding to cellular receptors. The spreading of the molecules is therefore governed, both, by an effective diffusion process and by the flow of Dpp-carrying cells. The cell flow is the result of tissue growth and cells divide in response to high local Dpp concentration. Hence, this model captures a feedback loop from morphogen concentration to cell division to tissue growth and back to morphogen transport.

Fig. 1. Drosophila wing primordium with Dpp morphogen profile visualized through the activated signal transducer pMad (green). Reproduced from Fig. 3A' (CC BY 4.0) by Schwank et al. (2011) PLoS Biol 9(7): e1001111.

In the referenced paper, Osborne et al. (2017) have compared five different model formalisms for multicellular tissues incl. the cellular Potts model (CPM) and had used the simulator Chaste. Here, the CPM-specific results (out of the five compared models) are reproduced in a different simulator, Morpheus, and both agree well.

Description

In the Morpheus model, the concentration c of Dpp is not described by a Global/Field (as it was done in the publication) but by a CellType/Property such that Dpp gets transported together with the cells by construction. Additionally, Dpp diffuses between neighboring cells which is implemented as a diffusion operator discretized over the cell arrangement by means of the NeighborhoodReporter.

All parameter values are taken from Tables 1 and 5 of the publication, except lambda=0.01 must have been a typo in the published Table 5 and is here replaced by lambda=10 as in the paper’s cited Ref.19 with the original model (Smith et al. (2011)).

A square lattice with 400x400 nodes and no-flux boundary conditions is used.

Results

A typical simulation run shows how the wing primordium grows from an initial circle to an ellipse with larger vertical axis than horizontal, in agreement with the published results. Also the heterogeneity of Dpp concentrations between cells is reproduced, see comparison and movie below.

Fig. 2. Comparison of simulation snapshots from Morpheus (top) and Chaste (bottom) at indicated time points. Dpp concentration is color-coded. Bottom panels are reproduced from [Fig. 10](https://doi.org/10.1371/journal.pcbi.1005387.g010) ([*CC BY 4.0*](https://creativecommons.org/licenses/by/4.0/): [**Osborne _et al._ (2017)**](#reference)). — Fig. 2. Comparison of simulation snapshots from Morpheus (top) and Chaste (bottom) at indicated time points. Dpp concentration is color-coded. Bottom panels are reproduced from Fig. 10 (*CC BY 4.0*: **Osborne *et al.* (2017)**).

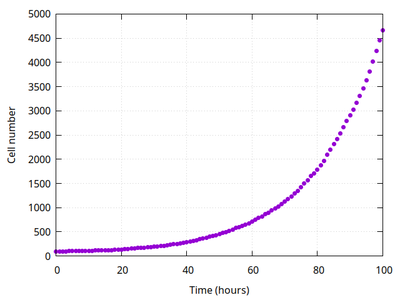
Fig. 3. Cell number time course of the Morpheus simulation run.

To quantitatively compare this pair of simulations, the horizontal Dpp profile and the aspect ratio of horizontal by vertical axis length are used. In the original publication, means were taken over 20 simulation runs but here we just compare to a single Morpheus run with plots generated by Morpheus during this simulation run.

Fig. 4. Quantitative comparison of simulation results from Morpheus (top) and Chaste (bottom). Left: Dpp concentration profiles as function of the x-location every 10 hours. Right: Aspect ratio of horizontal by vertical axis length as function of time. The published curves (bottom) represent statistics over 20 simulation runs with Chaste while just a single Morpheus run is shown (top). Moreover, the published Dpp profiles are averages over the y-coordinate across the tissue whereas, from the Morpheus run, values for all cell centers within the mid 2 percent of the lattice hight are shown (each dot corresponds to a cell, no average). Bottom panels are reproduced from [Fig. 11](https://doi.org/10.1371/journal.pcbi.1005387.g011) ([*CC BY 4.0*](https://creativecommons.org/licenses/by/4.0/): [**Osborne _et al._ (2017)**](#reference)). — Fig. 4. Quantitative comparison of simulation results from Morpheus (top) and Chaste (bottom). Left: Dpp concentration profiles as function of the x-location every 10 hours. Right: Aspect ratio of horizontal by vertical axis length as function of time. The published curves (bottom) represent statistics over 20 simulation runs with Chaste while just a single Morpheus run is shown (top). Moreover, the published Dpp profiles are averages over the y-coordinate across the tissue whereas, from the Morpheus run, values for all cell centers within the mid 2 percent of the lattice hight are shown (each dot corresponds to a cell, no average). Bottom panels are reproduced from Fig. 11 (*CC BY 4.0*: **Osborne *et al.* (2017)**).

Reference

This model reproduces a published result, originally obtained with a different simulator:

J. M. Osborne, A. G. Fletcher, J. M. Pitt-Francis, P. K. Maini, D. J. Gavaghan: Comparing individual-based approaches to modelling the self-organization of multicellular tissues. PLoS Comput. Biol. 13 (2): e1005387, 2017.

Model

Get this model via:

Morpheus-Link or

Download: Dpp_morphogen.xml

XML Preview

<?xml version='1.0' encoding='UTF-8'?>
<MorpheusModel version="4">
    <Description>
        <Details>Model ID:     https://identifiers.org/morpheus/M1703 
Software:     Morpheus (open source). Download from: https://morpheus.gitlab.io 
Full title:     Drosophila Wing Primordium 
Authors:      J. M. Osborne, A. G. Fletcher, J. M. Pitt-Francis, P. K. Maini, D. J. Gavaghan
Contributors: H. J. Wiederanders, P. H. Suhrcke, P. Rossbach
Submitter:    L. Brusch 
Curator:      J. Starruß, L. Brusch 
Date:           12.07.2020 
Reference:    J. M. Osborne, A. G. Fletcher, J. M. Pitt-Francis, P. K. Maini, D. J. Gavaghan: Comparing individual-based approaches to modelling the self-organization of multicellular tissues. PLoS Comput. Biol. 13 (2): e1005387, 2017. 
This model reproduces a published result, originally obtained with CHASTE, a different simulator. 
Comment:      All parameter values are taken from Tables 1 and 5 of the publication, except lambda=0.01 must have been a typo in the published Table 5 and is here replaced by lambda=10 as in the paper's cited Ref.19 (the original model from 2011).
</Details>
        <Title>Drosophila Wing Primordium</Title>
    </Description>
    <Space>
        <Lattice class="square">
            <Neighborhood>
                <Order>1</Order>
            </Neighborhood>
            <Size symbol="size" value="400, 400, 0"/>
            <BoundaryConditions>
                <Condition type="noflux" boundary="x"/>
                <Condition type="noflux" boundary="y"/>
            </BoundaryConditions>
        </Lattice>
        <SpaceSymbol symbol="space"/>
    </Space>
    <Time>
        <StartTime value="0"/>
        <StopTime value="100"/>
        <TimeSymbol symbol="time"/>
    </Time>
    <Global>
        <Constant symbol="stripe_pos" name="position of the production stripe in x dimension" value="size.x/2"/>
        <Constant symbol="c" value="0"/>
        <Constant symbol="CD" value="4"/>
        <Variable symbol="max.x" value="0"/>
        <Variable symbol="max.y" value="0"/>
        <Variable symbol="min.x" value="0"/>
        <Variable symbol="min.y" value="0"/>
        <Field symbol="Dpp" value="0"/>
    </Global>
    <CellTypes>
        <CellType name="cells" class="biological">
            <Constant symbol="dt" name="time step" value="0.005"/>
            <Constant symbol="D" name="Dpp diffusion coefficient" value="0.0001*CD*CD"/>
            <Constant symbol="k_c" name="Dpp degradation rate" value="0.01"/>
            <Constant symbol="p_div" name="average baseline cell division rate" value="0.1"/>
            <Constant symbol="lbd" name="morphogen effect on cell growth" value="10"/>
            <Constant symbol="L_prod" name="half width of stripe of Dpp production" value="2*CD"/>
            <Constant symbol="mu_g" name="cellular growth rate mean" value="0.05"/>
            <Constant symbol="var_g" name="cellular growth rate variance" value="0.0001"/>
            <Constant symbol="g_min" name="minimum cellular growth rate" value="0.01"/>
            <Property symbol="g" name="cell growth rate" value="max(g_min, rand_norm(mu_g,var_g))"/>
            <Property symbol="u" name="division probability weighting" value="rand_uni(0.1,0.2)"/>
            <Property symbol="c" name="Dpp concentration" value="0.0"/>
            <Property symbol="p" name="probability of division" value="0.0"/>
            <Property symbol="f" name="level of production of Dpp in stripe" value="0.0"/>
            <Property symbol="c_neighbor_mean" value="0.0"/>
            <Property symbol="d" name="nr. of divisions" value="0.0"/>
            <SurfaceConstraint target="4*CD" strength="0.01" mode="surface"/>
            <VolumeConstraint target="CD*CD" strength="0.1"/>
            <System time-step="dt" solver="Euler [fixed, O(1)]">
                <Rule symbol-ref="u">
                    <Expression>u*(1+dt*g*(1+lbd*c)*(1-u))</Expression>
                </Rule>
                <Rule symbol-ref="p">
                    <Expression>p_div*u*dt</Expression>
                </Rule>
                <Rule symbol-ref="f">
                    <Expression>if((cell.center.x > stripe_pos-L_prod) and (cell.center.x &lt; stripe_pos+L_prod), 0.01, 0)</Expression>
                </Rule>
                <DiffEqn symbol-ref="c">
                    <Expression>f-k_c*c+D*(4*c_neighbor_mean - 4*c)</Expression>
                </DiffEqn>
            </System>
            <CellDivision division-plane="random">
                <Condition>rand_uni(0,1) &lt; p</Condition>
                <Triggers name="">
                    <Rule symbol-ref="g">
                        <Expression>max(g_min, rand_norm(mu_g,var_g))</Expression>
                    </Rule>
                    <Rule symbol-ref="u">
                        <Expression>0.5*u</Expression>
                    </Rule>
                    <Rule symbol-ref="d">
                        <Expression>d+1</Expression>
                    </Rule>
                </Triggers>
            </CellDivision>
            <NeighborhoodReporter>
                <Input noflux-cell-medium="true" scaling="length" value="if(cell.type == celltype.cells.id, c,local.c)"/>
                <Output symbol-ref="c_neighbor_mean" mapping="average"/>
            </NeighborhoodReporter>
            <Mapper name="measure x-axis of tissue">
                <Input value="cell.center.x"/>
                <Output symbol-ref="max.x" mapping="maximum"/>
                <Output symbol-ref="min.x" mapping="minimum"/>
            </Mapper>
            <Mapper name="measure y-axis of tissue">
                <Input value="cell.center.y"/>
                <Output symbol-ref="max.y" mapping="maximum"/>
                <Output symbol-ref="min.y" mapping="minimum"/>
            </Mapper>
            <Mapper name="copy Dpp from cells into field for plotting">
                <Input value="c"/>
                <Output symbol-ref="Dpp"/>
            </Mapper>
        </CellType>
        <CellType name="medium" class="medium"/>
    </CellTypes>
    <CPM>
        <Interaction>
            <Contact type2="medium" type1="cells" value="0.2"/>
            <Contact type2="cells" type1="cells" value="0.1"/>
        </Interaction>
        <ShapeSurface scaling="norm">
            <Neighborhood>
                <Order>2</Order>
            </Neighborhood>
        </ShapeSurface>
        <MonteCarloSampler stepper="edgelist">
            <MCSDuration value="0.005"/>
            <MetropolisKinetics temperature="0.1"/>
            <Neighborhood>
                <Order>2</Order>
            </Neighborhood>
        </MonteCarloSampler>
    </CPM>
    <CellPopulations>
        <Population type="cells" size="1">
            <InitCircle mode="regular" number-of-cells="91">
                <Dimensions center="size.x/2,size.y/2,0" radius="5*CD"/>
            </InitCircle>
        </Population>
    </CellPopulations>
    <Analysis>
        <Gnuplotter time-step="5" name="Tissue with cell outlines and Dpp color-coded" decorate="true">
            <Plot>
                <Cells max="0.7" min="0" value="c">
                    <ColorMap>
                        <Color color="forest-green" value="0.7"/>
                        <Color color="gray" value="0.001"/>
                        <Color color="white" value="0"/>
                    </ColorMap>
                </Cells>
            </Plot>
            <Terminal name="png" size="1024, 1024, 0"/>
        </Gnuplotter>
        <Gnuplotter time-step="5" name="Tissue without cell outlines and just Dpp color-coded" decorate="true">
            <Plot>
                <Field symbol-ref="Dpp" max="0.7" min="0">
                    <ColorMap>
                        <Color color="forest-green" value="0.7"/>
                        <Color color="gray" value="0.001"/>
                        <Color color="white" value="0"/>
                    </ColorMap>
                </Field>
            </Plot>
            <Terminal name="png" size="1024, 1024, 0"/>
        </Gnuplotter>
        <Logger time-step="1">
            <Input/>
            <Output>
                <TextOutput/>
            </Output>
            <Plots>
                <Plot time-step="-1">
                    <Style grid="true" style="points"/>
                    <Terminal terminal="png"/>
                    <X-axis minimum="0" maximum="100">
                        <Symbol symbol-ref="Time"/>
                    </X-axis>
                    <Y-axis minimum="0">
                        <Symbol symbol-ref="Cell_number"/>
                    </Y-axis>
                </Plot>
                <Plot time-step="-1">
                    <Style grid="true" style="linespoints" point-size="0.5"/>
                    <Terminal terminal="png"/>
                    <X-axis>
                        <Symbol symbol-ref="Time"/>
                    </X-axis>
                    <Y-axis minimum="0.75" maximum="1.25">
                        <Symbol symbol-ref="aspect.published_max"/>
                        <Symbol symbol-ref="aspect.published_mean"/>
                        <Symbol symbol-ref="aspect.published_min"/>
                        <Symbol symbol-ref="aspect.Morpheus"/>
                    </Y-axis>
                </Plot>
            </Plots>
        </Logger>
        <Logger time-step="10">
            <Input/>
            <Output>
                <TextOutput/>
            </Output>
            <Plots>
                <Plot time-step="-1">
                    <Style style="points"/>
                    <Terminal terminal="png"/>
                    <X-axis minimum="-25" maximum="25">
                        <Symbol symbol-ref="x_location"/>
                    </X-axis>
                    <Y-axis minimum="0.0" maximum="0.7">
                        <Symbol symbol-ref="c"/>
                    </Y-axis>
                    <Color-bar palette="rainbow" minimum="0" maximum="100">
                        <Symbol symbol-ref="Time"/>
                    </Color-bar>
                </Plot>
            </Plots>
            <Restriction condition="cell.center.y>size.y*0.49 and cell.center.y&lt;size.y*0.51">
                <Celltype celltype="cells"/>
            </Restriction>
        </Logger>
        <ModelGraph include-tags="#untagged" reduced="false" format="svg"/>
        <Function symbol="Cell_number" name="Cell number">
            <Expression>celltype.cells.size</Expression>
        </Function>
        <Function symbol="Time" name="Time (hours)">
            <Expression>time</Expression>
        </Function>
        <Function symbol="aspect.published_max" name="XY Ratio, Paper (max)">
            <Expression>0.9725+0.0775*cos(pi*time/100)</Expression>
        </Function>
        <Function symbol="aspect.published_mean" name="XY Ratio, Paper (mean)">
            <Expression>0.94+0.06*cos(pi*time/100)</Expression>
        </Function>
        <Function symbol="aspect.published_min" name="XY Ratio, Paper (min)">
            <Expression>0.895+0.035*cos(pi*time/100)</Expression>
        </Function>
        <Function symbol="aspect.Morpheus" name="XY Ratio, Morpheus">
            <Expression>(max.x-min.x)/(max.y-min.y)</Expression>
        </Function>
        <Function symbol="x_location" name="x-location (CDs)">
            <Expression>(cell.center.x-size.x/2)/CD</Expression>
        </Function>
    </Analysis>
</MorpheusModel>

Downloads

Files associated with this model:

Last updated on Mon, 10 Feb 2025