Persistence

A. Czirók, K. Varga, E. Méhes, A. Szabó (Authors)

Persistent Identifier

Use this permanent link to cite or share this Morpheus model:

Introduction

This example shows self-organized collective motion of cells as a result of persistence (‘cellular inertia’). A similar model has recently been used by Czirók et al. (2013).

Persistence of individual cells causes self-organized collective motion.

Description

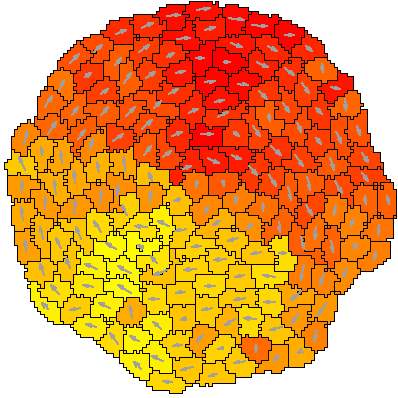
The model uses the Persistence plugin that causes cells to prefer to move in their current direction. The direction is stored in a PropertyVector that is used to plot the color and arrows in Gnuplotter.

The model is simulated in a circular domain with constant boundary conditions, which can be set up in Lattice/Domain/Circle. The value for the constant boundary is specified in CPM/BoundaryValue.

Things to try

Place static obstacles on the lattice and observe the flow pattern around the obstacle(s). The model included in the Morpheus-GUI has a corresponding CellType obstacle defined and already initializes a rectangular obstacle. To obtain the symmetric circular flow pattern in the video above, simply disable the initialization of the obstacle under CellPopulations.
Change the boundary conditions from circular$\ = \ $constant to $x/y = \ $periodic and observe the resulting collective motion.
Change the decay-time of Persistence (specifying the ‘memory’).

Reference

A. Czirók, K. Varga, E. Méhes, A. Szabó: Collective cell streams in epithelial monolayers depend on cell adhesion. New J. Phys. 15 (7): 075006, 2013.

Model

Get this model via:

Morpheus-Link or

Morpheus GUI: Examples → CPM → Persistence_2D.xml or

Download: Persistence_2D.xml

XML Preview

<MorpheusModel version="3">
    <Description>
        <Title>Example-Persistence</Title>
        <Details></Details>
    </Description>
    <Global>
        <VariableVector symbol="d" value="0.0, 0.0, 0.0" name="Moving direction"/>
        <Constant symbol="density" value="0.012"/>
    </Global>
    <Space>
        <Lattice class="square">
            <Size symbol="size" value="200, 200, 0"/>
            <Neighborhood>
                <Order>2</Order>
            </Neighborhood>
            <Domain boundary-type="constant">
                <Circle diameter="200"/>
            </Domain>
        </Lattice>
        <SpaceSymbol symbol="space"/>
    </Space>
    <Time>
        <TimeSymbol symbol="time"/>
        <StartTime value="0"/>
        <StopTime value="5000"/>
        <RandomSeed value="4"/>
    </Time>
    <CellTypes>
        <CellType class="biological" name="obstacle">
            <FreezeMotion>
                <Condition>1</Condition>
            </FreezeMotion>
        </CellType>
        <CellType class="biological" name="ct1">
            <PropertyVector symbol="d" value="0.0, 0.0, 0.0" name="Moving direction"/>
            <Property symbol="s" value="5"/>
            <VolumeConstraint target="100" strength="1"/>
            <SurfaceConstraint target="0.9" mode="aspherity" strength="1"/>
            <PersistentMotion protrusion="true" decay-time="50" strength="s"/>
            <MotilityReporter time-step="50">
                <Velocity symbol-ref="d"/>
            </MotilityReporter>
        </CellType>
        <CellType class="medium" name="medium"/>
    </CellTypes>
    <CPM>
        <Interaction>
            <Contact type1="ct1" type2="medium" value="16"/>
            <Contact type1="ct1" type2="ct1" value="1"/>
        </Interaction>
        <MonteCarloSampler stepper="edgelist">
            <MCSDuration value="1"/>
            <Neighborhood>
                <Order>2</Order>
            </Neighborhood>
            <MetropolisKinetics temperature="10"/>
        </MonteCarloSampler>
        <ShapeSurface scaling="norm">
            <Neighborhood>
                <Distance>3</Distance>
            </Neighborhood>
        </ShapeSurface>
    </CPM>
    <CellPopulations>
        <Population size="1" type="obstacle">
            <InitCellObjects mode="distance">
                <Arrangement repetitions="1, 1, 1" displacements="1, 1, 1">
                    <Box size="20,30,0" origin="130,100,0"/>
                </Arrangement>
            </InitCellObjects>
        </Population>
        <Population size="0" type="ct1">
            <InitCircle mode="regular" number-of-cells="400">
                <Dimensions radius="100" center="100, 100, 0"/>
            </InitCircle>
        </Population>
    </CellPopulations>
    <Analysis>
        <Gnuplotter time-step="100">
            <Terminal size="1000 600 0" name="png"/>
            <Plot>
                <Cells value="cell.id"/>
                <!--    <Disabled>
        <CellArrows style="1" orientation="3 * d / d.abs"/>
    </Disabled>
-->
            </Plot>
            <Plot>
                <Cells value="d.phi" min="0.0" max="6.28">
                    <ColorMap>
                        <Color value="6.28" color="red"/>
                        <Color value="3.14" color="blue"/>
                        <Color value="0.0" color="red"/>
                    </ColorMap>
                </Cells>
                <CellArrows style="1" orientation="3 * d / d.abs"/>
            </Plot>
        </Gnuplotter>
        <Logger time-step="10">
            <Input>
                <Symbol symbol-ref="cell.center.x"/>
                <Symbol symbol-ref="cell.center.y"/>
            </Input>
            <Output>
                <TextOutput file-separation="cell"/>
            </Output>
            <Plots>
                <Plot time-step="50">
                    <Style style="lines" line-width="2.0"/>
                    <Terminal terminal="png"/>
                    <X-axis minimum="0.0" maximum="size.x">
                        <Symbol symbol-ref="cell.center.x"/>
                    </X-axis>
                    <Y-axis minimum="0.0" maximum="size.y">
                        <Symbol symbol-ref="cell.center.y"/>
                    </Y-axis>
                    <Color-bar>
                        <Symbol symbol-ref="time"/>
                    </Color-bar>
                    <Range>
                        <Time mode="history" history="50"/>
                    </Range>
                </Plot>
            </Plots>
        </Logger>
    </Analysis>
</MorpheusModel>

Downloads

Files associated with this model:

Built-In Examples Cellular Potts Models

Last updated on Sat, 12 Dec 2020