ODEs in CPM Cells: Cell Cycle and Proliferation

Persistent Identifier

Use this permanent link to cite or share this Morpheus model:

ODE model of the Xenopus oocyte cell cycle coupled to 2D shaped CPM cells that perform divide based on component concentrations

Introduction

This multiscale model example shows

how to define a coupled system of continuous ODEs in discrete CPM cells,
how to specify and change time scales between these model formalisms.

Cells divide according to an oscillatory ODE model representing the early cell cycle in *Xenopus*.

Description

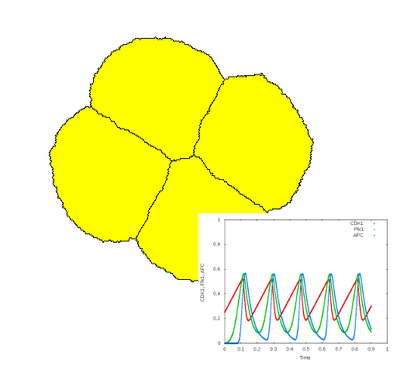
This model specifies an oscillatory ODE model representing the cell cycle in Xenopus oocytes using three components ($\text{CDK1}$, $\text{Plk1}$, $\text{APK}$) (Ferrell et al., 2011) (see CellTypes → CellType → System). This ODE model is coupled to 2D shaped CPM cells that perform divide based on the concentration of these components (see CellTypes → CellType → Proliferation → Condition). As in the early Xenopus cell cleavage, this leads to exponential growth of the number of cells, without increase of total cell volume.

Time scales

Time scales are defined in the following fashion:

The so-called global time scheme is defined in Time and here runs from $0$ to $1$ arbitrary time units. All models and plugins specify their updating scheme in terms this global time scheme (e.g. Analysis → Gnuplotter → Interval).
The CPM time scale for cell motility and behaviours is defined in CPM → MCSDuration. This specifies the time that a single Monte Carlo step in the CPM lasts, in terms of the ‘global time’. Here, the MCSDuration is $1.0\cdot10^{-4}$ which means the CPM is executed 10.000 times during this simulation.
For setting time of ODEs, one has to distinguish the (1) how often the ODEs are evaluated from (2) controlling the time scale of the ODE dynamics:
1. The time scale of the ODE dynamics can be changed using System → time-scaling. When larger or smaller than 1.0, this speeds up or slows down the dynamics without influencing the accuracy of the approximation.
2. The accuracy of the numerical approximation (and is equal to the $\Delta t$ of the numerical solver) is controlled using System → time-step (and is automatically rescaled according to the time scale).

Things to Try

Change the CPM time scale, relative to the ODE dynamics: Change CPM → MCSDuration to $1.0\cdot10^{-3}$ or decrease to $1.0\cdot10^{-5}$. This makes cells to have less resp. more motility/relaxation in between cell divisions.
Change the time scale of the ODE dynamics relative to the CPM by altering System → time-scaling.

Reference

J. E. Ferrell Jr., T. Y. Tsai, Q. Yang: Modeling the Cell Cycle: Why Do Certain Circuits Oscillate? Cell 144 (6): 874-885, 2011.

Model

Get this model via:

Morpheus-Link or

Morpheus GUI: Examples → Multiscale → CellCycle.xml or

Download: CellCycle.xml

XML Preview

<?xml version='1.0' encoding='UTF-8'?>
<MorpheusModel version="3">
    <Description>
        <Title>Example-CellCycle</Title>
        <Details>ODE model of Xenopus oocyte cell cycle adopted from:

James Ferrell, Tony Yu-Chen Tsai and Qiong Yang (2011) Modeling the Cell Cycle: Why Do Certain Circuits Oscillate?, Cell 144, p874-885. http://dx.doi.org/10.1016/j.cell.2011.03.006</Details>
    </Description>
    <Global/>
    <Space>
        <Lattice class="hexagonal">
            <Size symbol="size" value="250 250 0"/>
            <BoundaryConditions>
                <Condition boundary="x" type="periodic"/>
                <Condition boundary="y" type="periodic"/>
            </BoundaryConditions>
            <Neighborhood>
                <Order>1</Order>
            </Neighborhood>
        </Lattice>
        <SpaceSymbol symbol="space"/>
    </Space>
    <Time>
        <StartTime value="0"/>
        <StopTime value="1"/>
        <TimeSymbol symbol="time"/>
        <RandomSeed value="3445"/>
    </Time>
    <CellTypes>
        <CellType class="biological" name="cells">
            <Property symbol="CDK1" value="0" name="Cyclin-dependent kinase 1"/>
            <Property symbol="Plk1" value="0" name="Polo-like kinase 1"/>
            <Property symbol="APC" value="0" name="Anaphase-promoting complex"/>
            <System solver="runge-kutta" time-scaling="20" time-step="4e-2">
                <DiffEqn symbol-ref="CDK1">
                    <Expression>α1 - β1 * CDK1 * (APC^n / (K^n + APC^n))</Expression>
                </DiffEqn>
                <DiffEqn symbol-ref="Plk1">
                    <Expression>α2*(1-Plk1) * ((CDK1^n) / (K^n + CDK1^n)) - β2*Plk1</Expression>
                </DiffEqn>
                <DiffEqn symbol-ref="APC">
                    <Expression>α3*(1- APC) * ((Plk1^n) / (K^n + Plk1^n)) - β3*APC</Expression>
                </DiffEqn>
                <Constant symbol="n" value="8" name="Hill coefficient"/>
                <Constant symbol="K" value="0.5" name="Michaelis constant"/>
                <Constant symbol="α1" value="0.1"/>
                <Constant symbol="α2" value="3.0"/>
                <Constant symbol="α3" value="3.0"/>
                <Constant symbol="β1" value="3.0"/>
                <Constant symbol="β2" value="1.0"/>
                <Constant symbol="β3" value="1.0"/>
            </System>
            <Property symbol="p" value="0" name="portion"/>
            <Property symbol="d" value="0" name="divisions"/>
            <Property symbol="c" value="0" name="division timeout"/>
            <Property symbol="cc" value="1" name="cellcount"/>
            <Property symbol="Vt" value="25000" name="Target volume"/>
            <VolumeConstraint target="Vt" strength="1"/>
            <SurfaceConstraint target="1.0" mode="aspherity" strength="1"/>
            <Event>
                <Condition>CDK1&lt;0.2</Condition>
                <Rule symbol-ref="c">
                    <Expression>0</Expression>
                </Rule>
            </Event>
            <CellDivision division-plane="minor">
                <Condition>if(CDK1 > 0.5 and c == 0, 1, 0)</Condition>
                <Triggers>
                    <Rule symbol-ref="d">
                        <Expression>d+0.5</Expression>
                    </Rule>
                    <Rule symbol-ref="c">
                        <Expression>1</Expression>
                    </Rule>
                    <Rule symbol-ref="Vt">
                        <Expression>Vt/2</Expression>
                    </Rule>
                </Triggers>
            </CellDivision>
        </CellType>
    </CellTypes>
    <CPM>
        <Interaction default="0">
            <Contact type1="cells" type2="cells" value="-20"/>
        </Interaction>
        <MonteCarloSampler stepper="edgelist">
            <MCSDuration value="5e-5"/>
            <Neighborhood>
                <Order>1</Order>
            </Neighborhood>
            <MetropolisKinetics temperature="10" yield="0.1"/>
        </MonteCarloSampler>
        <ShapeSurface scaling="norm">
            <Neighborhood>
                <Order>3</Order>
            </Neighborhood>
        </ShapeSurface>
    </CPM>
    <CellPopulations>
        <Population size="0" type="cells">
            <InitCellObjects mode="order">
                <Arrangement repetitions="1, 1, 1" displacements="1, 1, 1">
                    <Sphere radius="40" center="125,100,0"/>
                </Arrangement>
            </InitCellObjects>
            <InitProperty symbol-ref="CDK1">
                <Expression>0.25</Expression>
            </InitProperty>
        </Population>
    </CellPopulations>
    <Analysis>
        <Gnuplotter time-step="0.05" decorate="false">
            <Terminal name="png"/>
            <Plot>
                <Cells value="CDK1">
                    <ColorMap>
                        <Color value="0.5" color="red"/>
                        <Color value="0.2" color="yellow"/>
                    </ColorMap>
                </Cells>
            </Plot>
        </Gnuplotter>
        <Logger time-step="2e-3">
            <Input>
                <Symbol symbol-ref="APC"/>
                <Symbol symbol-ref="CDK1"/>
                <Symbol symbol-ref="Plk1"/>
            </Input>
            <Output>
                <TextOutput file-format="csv"/>
            </Output>
            <Plots>
                <Plot time-step="-1">
                    <Style style="points" line-width="4.0"/>
                    <Terminal terminal="png"/>
                    <X-axis>
                        <Symbol symbol-ref="time"/>
                    </X-axis>
                    <Y-axis>
                        <Symbol symbol-ref="APC"/>
                        <Symbol symbol-ref="CDK1"/>
                        <Symbol symbol-ref="Plk1"/>
                    </Y-axis>
                </Plot>
                <Plot time-step="-1">
                    <Style style="points" line-width="4.0"/>
                    <Terminal terminal="png"/>
                    <X-axis>
                        <Symbol symbol-ref="CDK1"/>
                    </X-axis>
                    <Y-axis>
                        <Symbol symbol-ref="APC"/>
                    </Y-axis>
                    <Color-bar>
                        <Symbol symbol-ref="Plk1"/>
                    </Color-bar>
                </Plot>
            </Plots>
            <Restriction>
                <Celltype celltype="cells"/>
            </Restriction>
        </Logger>
    </Analysis>
</MorpheusModel>

Downloads

Files associated with this model:

Last updated on Sat, 12 Dec 2020