Delay Differential Equations: Cell Cycle
Persistent Identifier
Use this permanent link to cite or share this Morpheus model:
Introduction
This model is a two-species version of the Xenopus embryonic cell cycle shown above that uses delay differential equations (Ferrell et al., 2011). It exhibits sustained limit cycle oscillations.
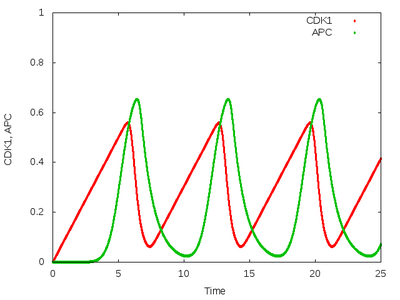
Description
This model uses two Properties ($\mathrm{CDK1}$ and $\mathrm{APC}$) and two DelayProperties ($\text{CDK1}_d$ and $\text{APC}_d$) with delay $\tau$. The latter are properties that return the value that has been assigned at time $t-\tau$.
The updated values of $\mathrm{CDK1}$ and $\mathrm{APC}$ are assigned to (the back of) $\text{CDK1}_d$ and $\text{APC}_d$ using Equations. When these properties used in the DiffEqn, they return the value assigned in the past.
The two variables are logged and both a time plot and a phase plot are drawn.
Things to try
- Explore the effect of delays by altering the
DelayProperty/delay.
Reference
J. E. Ferrell Jr., T. Y. Tsai, Q. Yang: Modeling the Cell Cycle: Why Do Certain Circuits Oscillate?. Cell 144 (6): 874-885, 2011.
Model
Examples → ODE → CellCycleDelay.xml or
CellCycleDelay.xml
XML Preview
<?xml version='1.0' encoding='UTF-8'?>
<MorpheusModel version="3">
<Description>
<Title>Example-CellCycleDelay</Title>
<Details>Example of delay differential equations.
Implements equation 23 and 24 and reproduces figure 7 from:
James Ferrell, Tony Yu-Chen Tsai and Qiong Yang (2011) Modeling the Cell Cycle: Why Do Certain Circuits Oscillate?, Cell 144, p874-885. http://dx.doi.org/10.1016/j.cell.2011.03.006</Details>
</Description>
<Global/>
<Space>
<Lattice class="linear">
<Size symbol="size" value="1 0 0"/>
<Neighborhood>
<Order>1</Order>
</Neighborhood>
</Lattice>
<SpaceSymbol symbol="space"/>
</Space>
<Time>
<StartTime value="0"/>
<StopTime value="25"/>
<SaveInterval value="0"/>
<TimeSymbol symbol="time"/>
</Time>
<CellTypes>
<CellType class="biological" name="cells">
<Property symbol="APC" value="0"/>
<Property symbol="CDK1" value="0"/>
<DelayProperty symbol="APC_d" value="0" delay="0.5"/>
<DelayProperty symbol="CDK1_d" value="0" delay="0.5"/>
<Equation symbol-ref="APC_d">
<Expression>APC</Expression>
</Equation>
<Equation symbol-ref="CDK1_d">
<Expression>CDK1</Expression>
</Equation>
<System solver="runge-kutta" time-scaling="1" time-step="1e-2">
<Constant symbol="n" value="8"/>
<Constant symbol="K" value="0.5"/>
<Constant symbol="α1" value="0.1"/>
<Constant symbol="α2" value="3.0"/>
<Constant symbol="β1" value="3.0"/>
<Constant symbol="β2" value="1.0"/>
<DiffEqn symbol-ref="CDK1">
<Expression>α1 - β1 * CDK1 * (APC_d^n) / (K^n + APC_d^n)</Expression>
</DiffEqn>
<DiffEqn symbol-ref="APC">
<Expression>α2*(1- APC) * ((CDK1_d^n) / (K^n + CDK1_d^n)) - β2*APC</Expression>
</DiffEqn>
</System>
</CellType>
</CellTypes>
<CellPopulations>
<Population size="1" type="cells"/>
</CellPopulations>
<Analysis>
<Logger time-step="1e-2">
<Restriction>
<Celltype celltype="cells"/>
</Restriction>
<Input>
<Symbol symbol-ref="APC"/>
<Symbol symbol-ref="APC_d"/>
<Symbol symbol-ref="CDK1"/>
<Symbol symbol-ref="CDK1_d"/>
</Input>
<Output>
<TextOutput/>
</Output>
<Plots>
<Plot time-step="-1">
<Style style="lines" line-width="3.0"/>
<Terminal terminal="png"/>
<X-axis>
<Symbol symbol-ref="time"/>
</X-axis>
<Y-axis>
<Symbol symbol-ref="CDK1"/>
<Symbol symbol-ref="CDK1_d"/>
<Symbol symbol-ref="APC"/>
<Symbol symbol-ref="APC_d"/>
</Y-axis>
</Plot>
</Plots>
</Logger>
</Analysis>
</MorpheusModel>
Downloads
Files associated with this model: